by Alexandra Cavallaro and Andrea Olinger
“Do problem sets count as writing?”
This was the question we asked Michael Loui, Professor of Electrical and Computer Engineering (ECE). His answer: a resounding yes. “It is actually a form of writing,” he said, “with diagrams and equations and all of that.”
Although students in his ECE classes might not be writing whole paragraphs in response to their homework problems, each solution needs to set up a chain of reasoning, to weave together words, symbols, and diagrams to make an argument. The kind of writing we see in problem sets shows up in the many different kinds of writing engineers do, such as technical specifications and documentation. Critically, this kind of writing also gives students opportunities to make their thinking and learning visible—something not possible from automatically graded multiple-choice homework.
One of Michael’s favorite problems, which he created for an introductory engineering exam, asks students to determine the efficiency of the Toyota Prius’s braking system (see part c in the image below). Students have to explain their reasoning—in words and mathematical formulas—because it will reveal whether they understand the problem. It turns out that if students make one mistake on this problem, they’ll get the wrong answer, but if they make two independent mistakes, applying two basic equations without checking the assumptions, they could get the right answer—“not a good thing in the real world,” Michael said. “So that’s why we want them to explain their reasoning.” (For those who are curious, the conceptual mistakes are described at the end of this post.)

An excerpt from Michael Loui’s Toyota Prius problem, where two mistakes might actually generate the right answer.
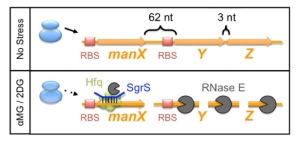
Writing like an electrical engineer—or a mathematician, or a microbiologist—means seeing equations, diagrams, and models not as auxiliary elements but as key components of the argument. In a co-authored article for PNAS, for example, Associate Professor of Microbiology Cari Vanderpool pointed out that the first figure, a cartoon model, illustrates a hypothesis that ends up being disproven:
In an interview, Cari noted that she had initially worried that this image might give the hypothesis too much emphasis, but she ultimately decided to include it “because people would be set up with some of the basics about how the genes were organized.”
“Students don’t always realize you need things like this,” Cari said, “but when you’re reading a paper, if you don’t have this, saying all this in words becomes way too cumbersome, and it’s too hard to follow the relevant parts of the tools that are being used. You need some kind of relevant illustration…to easily understand what’s being done in the experiment.” She said that when she reads articles and has to keep track of different conditions, she ends up taking notes and drawing cartoons herself. “So when I write,” she said, “I try to make that easier for the reader and just provide them with that visual cue to different constructs so they don’t have to do their own little cartoons.”
For those of you who teach STEM courses, do your students have opportunities to compose with visuals or argue with equations? Many STEM students, Michael said, see writing as “what their English teachers teach them.” When the practices we have described are seen as forms of composing, persuading, and arguing, how does that change how you teach and how your students approach their work? Let us know in the comments.
A Few Resources on Writing in STEM
- An Engineer’s Guide to Technical Communication (2006), by Sheryl Sorby and William Bulleit, Michigan Tech (written by engineers, and recommended by Michael as the only text that “shows what real engineers actually do)
- Student Writing in the Quantitative Disciplines: A Guide for College Faculty (2012), by Patrick Bahls, UNC Asheville (an exciting new book on various aspects of writing pedagogy in STEM, from low-stakes writing to formal writing projects; see a Profhacker review here)
- STEM Database on the WAC Clearinghouse (a bibliography on how STEM writers learn the specialized writing practices of their disciplines and professions, as well as writing-to-learn pedagogy)
*In an email, Michael explained that students can make two conceptual mistakes on part (c) and wind up with the correct answer as follows:
1. Average power equals Vrms times Irms. (rms denotes “root mean square”)
2. The rms value equals the peak (maximum) value divided by the square root of 2.
3. So Pavg = (290/sqrt(2)) x (30/sqrt(2)) = 4350.
Statement #1 is true only in special circumstances, such as when the current is proportional to the voltage. In this problem, the current decreases from 0 to 4 sec, and the voltage is constant. Statement #2 is true only for alternating current, but the electrical system in the problem uses direct current. In other words, students can apply two basic equations without checking the assumptions and produce the correct answer.